决策树
1.概述
基本上决策树都是二叉树
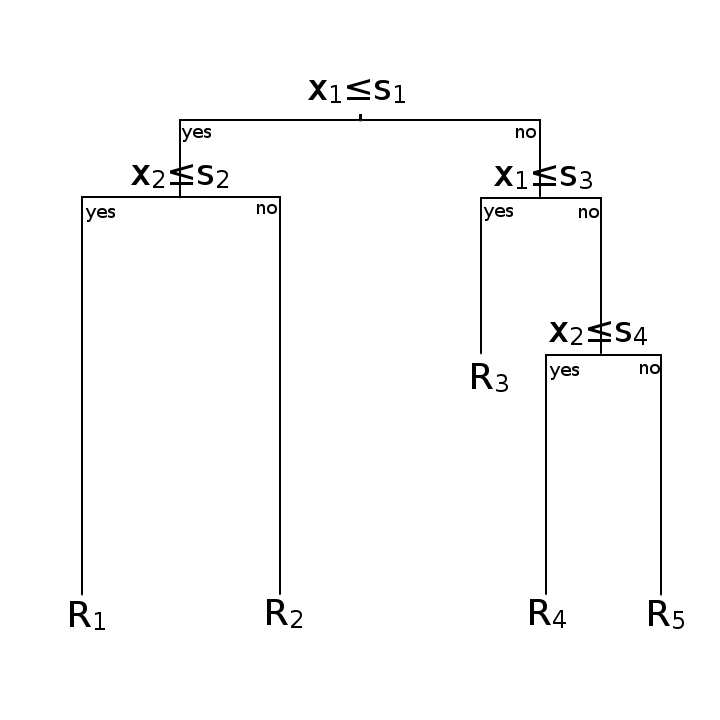
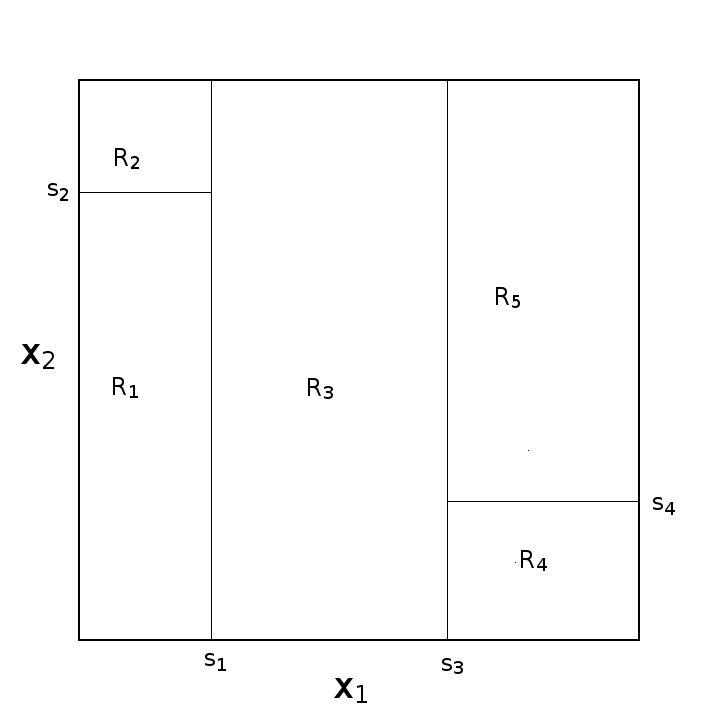
两幅图意思一样
2.决策树 vs 逻辑回归
最大的差异上图就可以看出,左边为逻辑回归的决策面,右边为决策树的决策面
3.构建算法
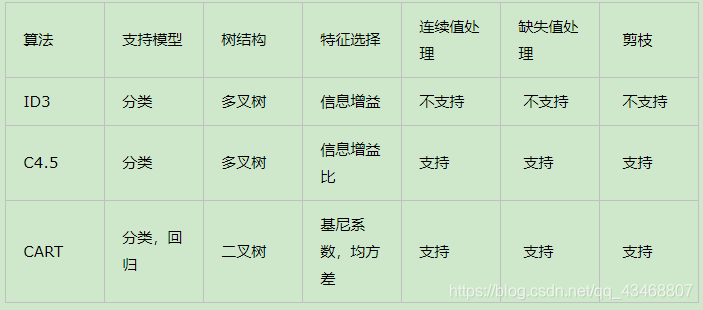
常见方法的有ID3,C4.5,CART,总结如下

3.1 ID3
假设训练数据集为 $D$,∣$D∣$表示其大小。设有$K$个分类$ C_1,C_2,…,C_K$。设特征集为$\textbf{A}$,假设某个特征$ A$ 有$ n$ 个不同的取值 $\{a_1,a_2,…,a_n\}$,根据特征$A$的取值将 $D$ 划分成$n$个子集。记子集 $D_i$中属于类$ C_k$的样本集合为 $D_{ik}$。
数据集$D$的经验熵$H(D)$:
特征$A$对数据集$ D$的经验条件熵$H(D|A)$
信息增益$g(D,A)$
算法流程:
- 若$D$中所有实例都属于同一类 $C_k$,则 $T$ 为单节点树,并将类 $C_k$作为该节点的类标记,返回$T$.
- 若$\textbf{A}=\phi$,则$T$为单节点树,并将$D$中实例最大的类$C_k$作为该节点的类标记,返回$T$.
- 否则,按照信息增益的算法,计算每个特征对$D$的信息增益,取信息增益最大的特征 $A_g$.
- 如果$A_g< \varepsilon$,则置 $T$为单节点树,并将$D$中实例最大的类$C_k$作为该节点的类标记,返回$T$.
- 否则,对$A_g$的每一可能值 $a_i$,依$A_g=a_i$将$D$分成若干非空子集$D_i$
- 以$D_i$为训练集,以$\textbf{A}- A_g $为特征集,递归地调用步骤1到步骤5,得到子树 $T_i$,全部 $T_i$构成$T$,返回$T$.
3.2 C4.5
C4.5算法流程与ID3相类似,只不过将信息增益改为信息增益比,以解决偏向取值较多的属性的问题,另外它可以处理连续型属性。
分裂信息 $SplitInformation(D,A)$
信息增益比 $GainRatio(D, A)$
3.3 CART
3.3.1 CART分类树
CART分类树算法使用基尼系数来代替信息增益(比),基尼系数代表了模型的不纯度,基尼系数越小,不纯度越低,特征越好。这和信息增益(比)相反。
对于样本$D$,个数为$|D|$,假设$K$个类别,第$k$个类别的数量为$|C_k|$,则样本$D$的基尼系数表达式:
对于样本$D$,个数为$|D|$,根据特征$A$的某个值$a$,把$D$分成$|D_1|$和$|D_2|$,则在特征$A=a$的条件下,样本$D$的基尼系数表达式为:
算法流程:算法输入训练集$D$,基尼系数的阈值,样本个数阈值。输出的是决策树$T$。
(1)、对于当前节点的数据集为$D$,如果样本个数小于阈值或没有特征,则当前节点停止递归,返回决策树。
(2)、计算样本集$D$的基尼系数,如果基尼系数小于阈值,则当前节点停止递归,返回决策树。
(3)、计算当前节点所有特征的各个特征值对数据集$D$的基尼系数
(4)、在计算出来的所有基尼系数中,选择基尼系数最小的特征$A$和对应的特征值$a$,并把数据集划分成两部分$D_1$和$D_2$,同时建立当前节点的左右节点,左节点的数据集$D$为$D_1$,右节点的数据集$D$为$D_2$。
(5)、对左右的子节点递归的调用1-4步,生成决策树。
3.3.2 CART回归树
对回归树用平方误差最小化准则
算法流程:输入为训练数据$D$,输出为回归树$f(x)$
(1) 选择最优的切分变量$j$和切分点$s$,遍历$j$,对固定的$j$遍历$s$,求解
(2) 用选定的$(j,s)$划分区域并决定输出值
(3) 继续对两个子区域调用步骤(1)(2),直至满足停止条件
(4) 将输入空间划分成$M$个区域$R_1,R_2,…,R_M$,生成回归树
3.4 多变量决策树
无论ID3,C4.5,CART都是选择一个最优的特征做分类决策,但大多数,分类决策不是由某一个特征决定,而是一组特征。这样得到的决策树更加准确,这种决策树叫多变量决策树(multi-variate decision tree)。在选择最优特征的时,多变量决策树不是选择某一个最优特征,而是选择一个最优的特征线性组合做决策。
代表算法OC1。
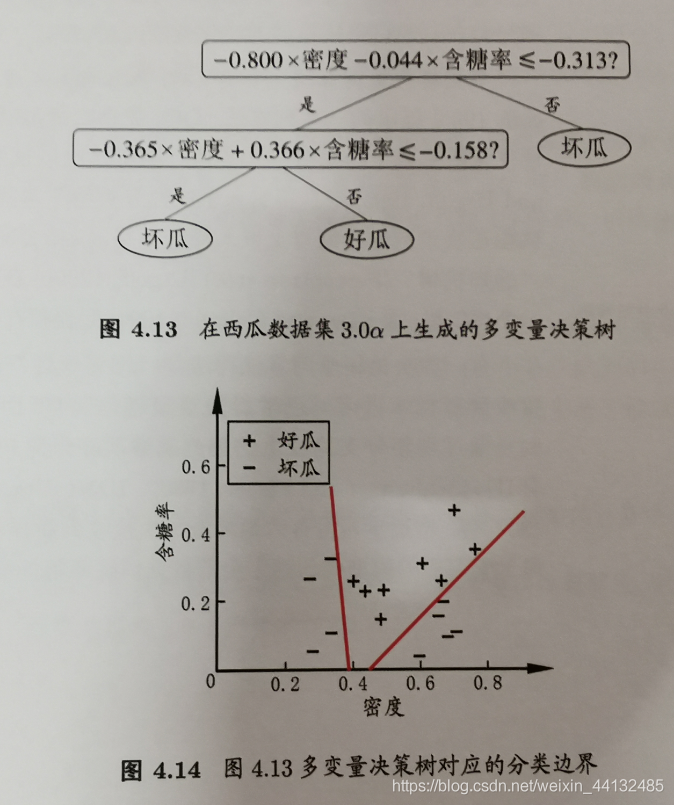
4.剪枝
剪枝(pruning)是解决决策树过拟合的主要手段,通过剪枝可以大大提升决策树的泛化能力。通常,剪枝处理可分为:预剪枝,后剪枝。
- 预剪枝:通过启发式方法,在生成决策树过程中对划分进行考察,若当前结点的划分影响决策树的泛化性能,则停止划分,并将其标记为叶节点
- 后剪枝:对已有的决策树,自底向上的对非叶结点进行考察,若该结点对应的子树替换为叶结点能提升决策树的泛化能力,则将改子树替换为叶结点
参考
https://zhuanlan.zhihu.com/p/89607509
https://www.cnblogs.com/wxquare/p/5379970.html
https://blog.csdn.net/qq_43468807/article/details/105969232
http://leijun00.github.io/2014/09/decision-tree/
https://zhuanlan.zhihu.com/p/89607509
https://www.cnblogs.com/wxquare/p/5379970.html
https://blog.csdn.net/qq_43468807/article/details/105969232
http://leijun00.github.io/2014/09/decision-tree/
https://www.cnblogs.com/wqbin/p/11689709.html
https://www.cnblogs.com/keye/p/10564914.html
https://www.cnblogs.com/keye/p/10601501.html
https://cloud.tencent.com/developer/article/1486712
https://blog.csdn.net/weixin_44132485/article/details/106502422
1.前馈神经网络
2.感知机
3.逻辑回归
4.神经网络进行二分类时,输出层使用两个神经元和只使用一个神经元,模型的性能有何差异,为什么?
5.分类算法之朴素贝叶斯
6.分类回归模型总结
7.深度学习中的五种归一化(BN、LN、IN、GN和SN)方法简介
8.CRF和HMM

