https://zhuanlan.zhihu.com/p/138107999

https://blog.csdn.net/txwh0820/article/details/51791739

1.定义

就是利用已知的样本结果信息，反推最具有可能导致这些样本结果出现的模型参数值。换句话说，即：“模型已定，结果已知，反推参数”。

2.极大似然构造损失函数

大多数常见的损失函数就是基于极大似然推导的。例子参考 https://www.cnblogs.com/hello-ai/p/11000899.html

判别模型下的极大似然估计

最大似然估计很容易扩展到估计条件概率$P\left (y|x;\theta \right)$，从而给定$x$预测$y$。实际上这是最常见的情况，因为这构成了大多数监督学习的基础。如果$X$表示所有的输入，$Y$表示我们观测到的目标，那么条件最大似然估计是：

$$\theta_{ML} = \mathop\arg\max_{\theta}P\left(Y|X;\theta \right)$$

如果假设样本是独立同分布的，那么这可以分解成

$$\theta_{ML} = \mathop\arg\max_{\theta}\sum_{i=1}^m logP\left(y^{(i)}|x^{(i)};\theta \right)$$

生成模型下的极大似然估计

考虑一组含有m个样本的数据集$X = \left \{ x^{(1)}, …, x^{(m)} \right \}$，由$p_{data}(x)$生成，独立同分布

对独立同分布的样本，生成样本集$X$的概率如下:

$$p_{model}(X; \theta)= \prod _{i=1}^m p_{model}\left (x^{(i)}; \theta \right )$$

对$\theta$的最大似然估计被定义为：

$$\theta_{ML} = \mathop{\arg\max}_{\theta}p_{model}\left (X;\theta \right ) = \mathop{\arg\max}_{\theta}\prod _{i=1}^m p_{model}\left (x^{(i)}; \theta \right )$$

多个概率的乘积公式会因很多原因不便于计算。例如，计算中很可能会因为多个过小的数值相乘而出现数值下溢。为了得到一个便于计算的等价优化问题，两边取对数：

$$\theta_{ML} = \mathop{\arg\max}_{\theta}\sum_{i=1}^{m}logp_{model}\left (x^{(i)};\theta\right )$$

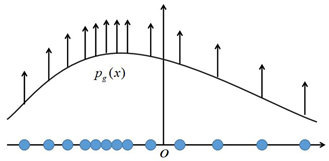
可以发现，使用极大似然估计时，每个样本$x^{(i)}$都希望拉高它所对应的模型概率值$p_{model}(x^{(i)};\theta)$，如上图所示，但是由于所有样本的密度函数$p_{model}(x^{(i)};\theta)$的总和必须是1，所以不可能将所有样本点都拉高到最大的概率，一个样本点的概率密度函数值被拉高将不可避免的使其他点的函数值被拉低，最终的达到一个平衡态。我们也可以将上式除以$m$，便可以看到极大似然法最大化的目标是在经验分布$\widehat{p}_{data}$下样本概率对数的期望值，即

$$\theta_{ML} = \mathop{\arg\max}_{\theta}E_{x\sim \widehat{p}_{data}}logp_{model}\left (x^{(i)};\theta \right )$$

参考

https://zhuanlan.zhihu.com/p/26614750

https://www.cnblogs.com/hello-ai/p/11000899.html

https://blog.csdn.net/hustqb/article/details/77168436

https://zhuanlan.zhihu.com/p/273246971

$P(X=玩 lol)=0.6；P(X=不玩lol)=0.4$，这个概率是统计得到的,或者你自身依据经验给出的一个概率值，我们称其为先验概率(prior probability)；

$P(X=玩lol|Y=男性)$称之为$X$的后验概率，即它获得是在观察到事件$Y=男性$发生后得到的

参考

https://zhuanlan.zhihu.com/p/26464206

GAN需要KL散度和JS散度，所以先预热。

1.熵

信息量为：

$$\begin{align} I(x) &= - \log(p(x)) \tag{1} \end{align}$$

熵为信息量的算术平均：

$$H(x) = - \sum_{i=1}^{n}p(x_i)log(p(x_i)) \tag{2}$$

2.交叉熵

交叉熵为

$$H(P,Q) = -\sum_{i=1}^np(x_i)logq(x_i)\tag{3}$$

3.KL散度

对于同一个随机变量有两个单独的概率分布，我们可以使用KL散度(Kullback-Leibler divergence)来衡量两个分布的差异。在机器学习的损失函数的计算中，我们可以假设$P$为样本的真实分布，$Q$用来表示模型所预测的分布，使用KL散度来衡量两个分布之间的差异。KL散度等于交叉熵减去熵

$$\begin{align} D_{KL}(P||Q) &= \sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)}) \notag\\ &=\sum_{i=1}^np(x_i)(logp(x_i)-logq(x_i)) \notag\\ &=\sum_{i=1}^n[p(x_i)logp(x_i)-p(x_i)logq(x_i)] \notag\\ &=\sum_{i=1}^np(x_i)logp(x_i)-\sum_{i=1}^np(x_i)logq(x_i) \\ &=-H(P)+H(P,Q)\tag{4} \end{align}$$

$P$和$Q$概率分布越接近，$D_{KL}(P||Q)$越小。

KL散度与交叉熵区别与联系

https://blog.csdn.net/Dby_freedom/article/details/83374650

KL散度主要有两个性质：

（1）不对称性

尽管KL散度从直观上是个距离函数，但它并不是一个真正的度量，因为它不具有对称性，即$D_{KL}(P||Q)\neq D_{KL}(Q||P)$。

（2）非负性

即$D_{KL}(P||Q) \geq 0$。

4.JS散度

JS散度也是用于度量两个概率分布的相似度，其解决了KL散度不对称的缺点

$$JS(P||Q) = \frac{1}{2}KL(P||\frac{P+Q}{2})+\frac{1}{2}KL(Q||\frac{P+Q}{2}) \tag{5}$$

不同于KL主要在两方面：

（1）值域范围

JS散度的值域范围是[0,1]，相同则是0，相反为1。

（2）对称性

即$ JS(P||Q)=JS(Q||P)$，从数学表达式中就可以看出。

参考

https://www.cnblogs.com/Mrfanl/p/11938139.html

https://zhuanlan.zhihu.com/p/346518942

https://www.w3cschool.cn/article/83016451.html