1.梯度
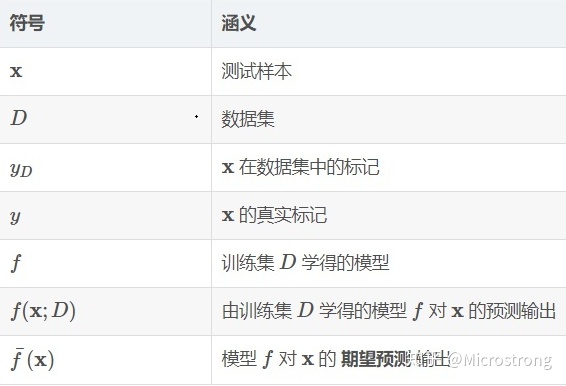
设二元函数$z=f(x,y)$ 在平面区域$D$上具有一阶连续偏导数,则对于每一个点$P(x,y)$的梯度为
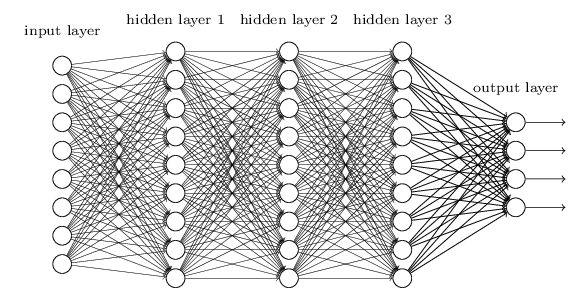
2.BP算法图示
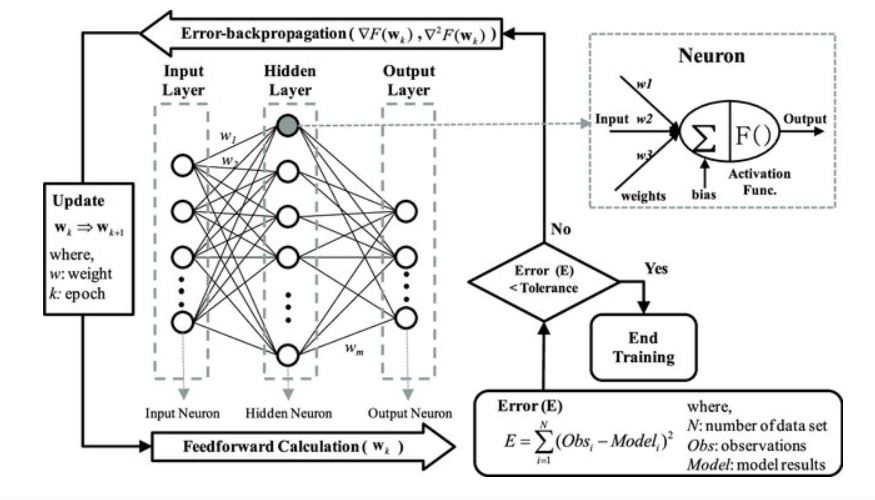
3.梯度消失和梯度爆炸
梯度爆炸和梯度消失问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。
举个例子,现有如上链式连接的网络$(x\rightarrow z \rightarrow y)$
假设$g$为sigmoid,那么$g^{‘}(z)$最大值为$\frac{1}{4}$,而我们初始化的网络权值通常都小于1,所以$g^{‘}(z)w \le \frac{1}{4}$,因此对于上面的链式求导,层数越多,求导结果$\frac{\partial C }{\partial b_1}$越小,因而导致梯度消失的情况出现。
这样,梯度爆炸问题的出现原因就显而易见了,当$w$比较大的时候或者激活函数的梯度较大,即$g^{‘}(z)w > 1$,层数越多,求导结果$\frac{\partial C }{\partial b_1}$越大,直到爆炸。
4.梯度消失和梯度爆炸解决方法
4.1 解决梯度消失
1.用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。
2.用Batch Normalization。
3.LSTM的结构设计也可以改善RNN中的梯度消失问题。
4.残差网络
5.合适的初始化权重
4.2解决梯度爆炸
1.梯度剪切:对梯度设定阈值
2.权重正则化(L1 和 L2 )
3.合适的初始化权重
参考
https://www.analyticsvidhya.com/blog/2021/06/the-challenge-of-vanishing-exploding-gradients-in-deep-neural-networks/
https://zhuanlan.zhihu.com/p/25631496
https://aijishu.com/a/1060000000100195