k-fold
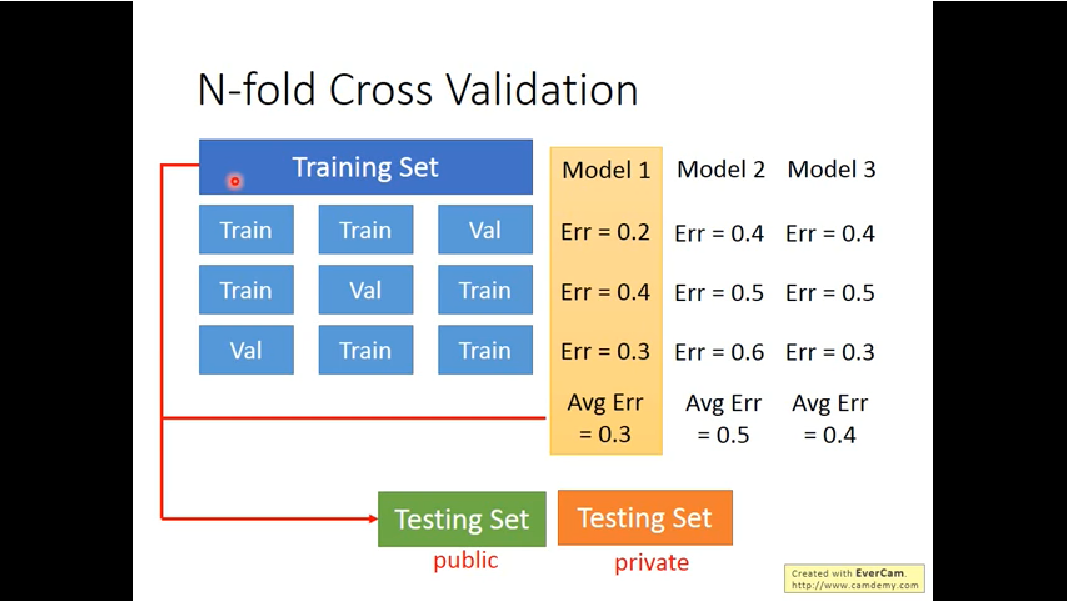
大佬写的很详细,Mark一下
https://www.cnblogs.com/pinard/p/7048333.html
https://zhuanlan.zhihu.com/p/148813079#
KNN可以用来分类和回归,以分类为例。
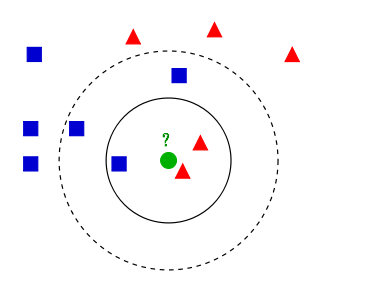
KNN分类算法的计算过程:
1)计算待分类点与已知类别的点之间的距离
2)按照距离递增次序排序
3)选取与待分类点距离最小的K个点
4)确定前K个点所在类别的出现次数
5)返回前K个点出现次数最高的类别作为待分类点的预测分类
如上图,举个例子:
1.闵可夫斯基距离
2.欧式距离
3.曼哈顿距离
选择较小的K值,容易发生过拟合;选择较大的K值,则容易欠拟合。在应用中,通常采用交叉验证法来选择最优K值。
优点:
1)算法简单,理论成熟,既可以用来做分类也可以用来做回归。
2)可用于非线性分类。
缺点:
1)需要算每个测试点与训练集的距离,当训练集较大时,计算量相当大,时间复杂度高,特别是特征数量比较大的时候。
2)样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少),对稀有类别的预测准确度低。
线性回归是解决回归任务的线性模型
LR是二分类模型,在线性模型的基础上加入激活函数sigmoid,适用在线性可分的二分类任务
简单总结:1.对于完全线性可分,硬间隔 2.不能够完全线性可分,引入松弛变量 ,软间隔 3.线性不可分,引入核函数
原理可参考: https://zhuanlan.zhihu.com/p/77750026 或者 https://blog.csdn.net/qq_37321378/article/details/108807595
核函数 https://blog.csdn.net/mengjizhiyou/article/details/103437423
原文地址 https://cseweb.ucsd.edu/classes/fa17/cse291-b/reading/Rendle2010FM.pdf
https://zhuanlan.zhihu.com/p/50426292
a new model class that combines the advantages of Support Vector Machines (SVM) with factorization models
In total, the advantages of our proposed FM are:
1) FMs allow parameter estimation under very sparse data where SVMs fail.
2) FMs have linear complexity, can be optimized in the primal and do not rely on support vectors like SVMs.
3) FMs are a general predictor that can work with any real valued feature vector.
1) 模型:
$x_i$表示第$i$个特征,但是针对上式,一个很大的问题,用户交互矩阵往往是比较稀疏的,这样就会导致对$w_{i,j}$的估算存在很大的问题。举个例子,假如想要估计Alice(A)和Star Trek(ST)的交互参数$w_{A,ST}$,由于训练集中没有实例同时满足$x_A$和$x_{ST}$非零,这会造成$w_{A,ST}=0$。因此这里使用了矩阵分解的思想:
2) 提升效率:
直接计算上面的公式求解$\hat{y}(x)$的时间复杂度为$O ( k n^2 ) $,因为所有的特征交叉都需要计算。但是可以通过公式变换,将时间复杂度减少到$O(kn)$,如下公式推导
FM can be applied to a variety of prediction tasks. Among them are: Regression,Binary classification,Ranking
the model parameters of FMs can be learned efficiently by gradient descent methods – e.g. stochastic gradient descent (SGD).The gradient of the FM model is:
The 2-way FM described so far can easily be generalized to a d-way FM:
直接计算上式的时间复杂度为$O(k_dn^d)$,利用类似上面的公式变形也可以将其降低为$O(k_d n )$
FMs model all possible interactions between values in the feature vector $x$ using factorized interactions instead of full parametrized ones. This has two main advantages:
1) The interactions between values can be estimated even under high sparsity. Especially, it is possible to generalize to unobserved interactions.
2) The number of parameters as well as the time for prediction and learning is linear.
Features with sparse data are features that have mostly zero values. This is different from features with missing data.
Common problems with sparse features include:
Removing features from the model
Make the features dense
Using models that are robust to sparse features
基本上决策树都是二叉树
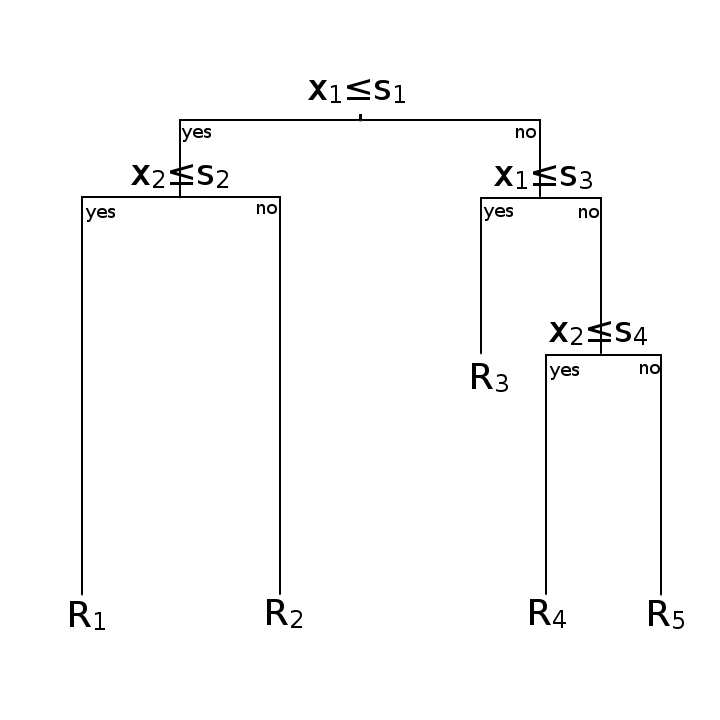
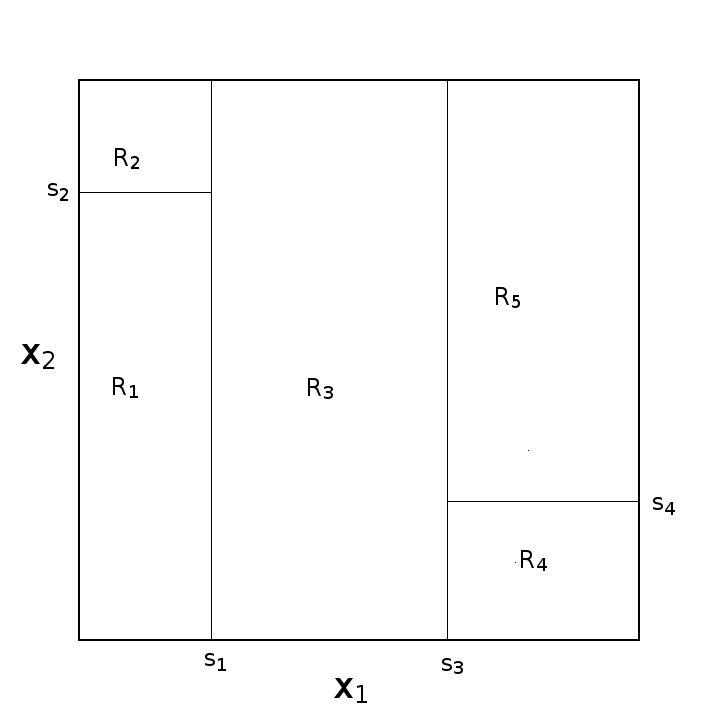
两幅图意思一样
最大的差异上图就可以看出,左边为逻辑回归的决策面,右边为决策树的决策面
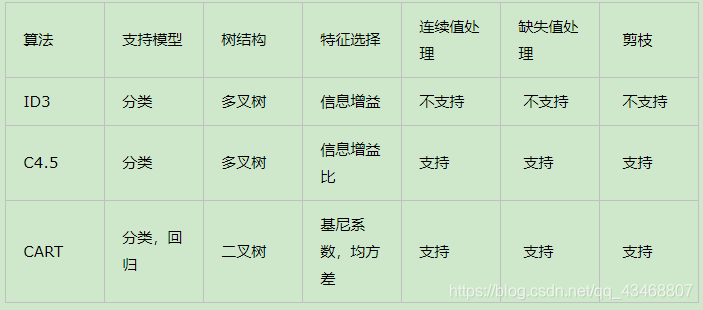
常见方法的有ID3,C4.5,CART,总结如下

假设训练数据集为 $D$,∣$D∣$表示其大小。设有$K$个分类$ C_1,C_2,…,C_K$。设特征集为$\textbf{A}$,假设某个特征$ A$ 有$ n$ 个不同的取值 $\{a_1,a_2,…,a_n\}$,根据特征$A$的取值将 $D$ 划分成$n$个子集。记子集 $D_i$中属于类$ C_k$的样本集合为 $D_{ik}$。
数据集$D$的经验熵$H(D)$:
特征$A$对数据集$ D$的经验条件熵$H(D|A)$
信息增益$g(D,A)$
算法流程:
C4.5算法流程与ID3相类似,只不过将信息增益改为信息增益比,以解决偏向取值较多的属性的问题,另外它可以处理连续型属性。
分裂信息 $SplitInformation(D,A)$
信息增益比 $GainRatio(D, A)$
CART分类树算法使用基尼系数来代替信息增益(比),基尼系数代表了模型的不纯度,基尼系数越小,不纯度越低,特征越好。这和信息增益(比)相反。
对于样本$D$,个数为$|D|$,假设$K$个类别,第$k$个类别的数量为$|C_k|$,则样本$D$的基尼系数表达式:
对于样本$D$,个数为$|D|$,根据特征$A$的某个值$a$,把$D$分成$|D_1|$和$|D_2|$,则在特征$A=a$的条件下,样本$D$的基尼系数表达式为:
算法流程:算法输入训练集$D$,基尼系数的阈值,样本个数阈值。输出的是决策树$T$。
(1)、对于当前节点的数据集为$D$,如果样本个数小于阈值或没有特征,则当前节点停止递归,返回决策树。
(2)、计算样本集$D$的基尼系数,如果基尼系数小于阈值,则当前节点停止递归,返回决策树。
(3)、计算当前节点所有特征的各个特征值对数据集$D$的基尼系数
(4)、在计算出来的所有基尼系数中,选择基尼系数最小的特征$A$和对应的特征值$a$,并把数据集划分成两部分$D_1$和$D_2$,同时建立当前节点的左右节点,左节点的数据集$D$为$D_1$,右节点的数据集$D$为$D_2$。
(5)、对左右的子节点递归的调用1-4步,生成决策树。
对回归树用平方误差最小化准则
算法流程:输入为训练数据$D$,输出为回归树$f(x)$
(1) 选择最优的切分变量$j$和切分点$s$,遍历$j$,对固定的$j$遍历$s$,求解
(2) 用选定的$(j,s)$划分区域并决定输出值
(3) 继续对两个子区域调用步骤(1)(2),直至满足停止条件
(4) 将输入空间划分成$M$个区域$R_1,R_2,…,R_M$,生成回归树
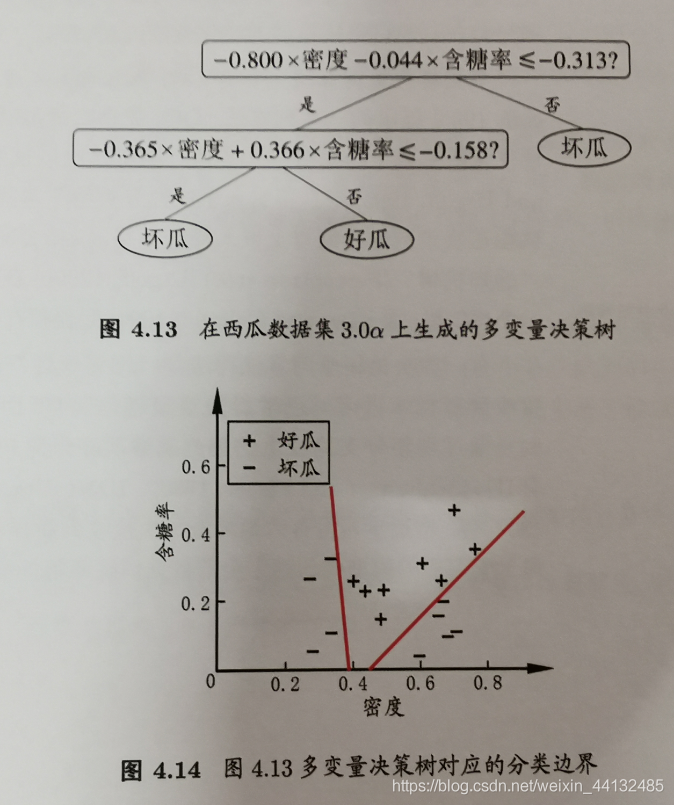
无论ID3,C4.5,CART都是选择一个最优的特征做分类决策,但大多数,分类决策不是由某一个特征决定,而是一组特征。这样得到的决策树更加准确,这种决策树叫多变量决策树(multi-variate decision tree)。在选择最优特征的时,多变量决策树不是选择某一个最优特征,而是选择一个最优的特征线性组合做决策。
代表算法OC1。
剪枝(pruning)是解决决策树过拟合的主要手段,通过剪枝可以大大提升决策树的泛化能力。通常,剪枝处理可分为:预剪枝,后剪枝。
https://zhuanlan.zhihu.com/p/89607509
https://www.cnblogs.com/wxquare/p/5379970.html
https://blog.csdn.net/qq_43468807/article/details/105969232
http://leijun00.github.io/2014/09/decision-tree/
https://zhuanlan.zhihu.com/p/89607509
https://www.cnblogs.com/wxquare/p/5379970.html
https://blog.csdn.net/qq_43468807/article/details/105969232
http://leijun00.github.io/2014/09/decision-tree/
https://www.cnblogs.com/wqbin/p/11689709.html
https://www.cnblogs.com/keye/p/10564914.html
https://www.cnblogs.com/keye/p/10601501.html
https://cloud.tencent.com/developer/article/1486712
https://blog.csdn.net/weixin_44132485/article/details/106502422
1.高纬空间样本具有稀疏性,容易欠拟合
2.可视化
3.维度过大导致训练时间长,预测慢
大致分为线形降维度和非线性降维,线形降维包括PCA,LDA等,非线性降维包括LLE,t-SNE,auto encoder等。
假设矩阵$x\in \mathbb{R}^{ n}$,假设有$M$个样本,将原始数据按列组成$M$ 行$ n $列矩阵$ X\in \mathbb{R}^{M\times n}$,PCA的使用过程为:
1.计算协方差矩阵$G_t \in \mathbb{R}^{n \times n}$
注意,其中$\overline{X}\in \mathbb{R}^{n}$为列的均值,$X-\overline{X}$表示将$ X$ 的每一列进行零均值化,即减去这一列的均值
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列,取前 $k$ 列组成矩阵 $P\in \mathbb{R}^{n \times k} $
4.实现数据降维
局限:
a. PCA只能针对1D的向量,对于2D的矩阵而言,比如图片数据,需要先flatten成向量
将2D的矩阵flatten成向量其实丢失了行列的位置信息,为了直接在2D的矩阵上实现降维,提出了2DPCA。
假设有原始矩阵$A\in\mathbb{R}^{m \times n }$,使用过程如下:
1.计算协方差矩阵
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列,取前 $k$ 列组成矩阵
4.实现数据降维
作者证明了2DPCA只是在行上工作,然后提出了Alternative 2DPCA可以工作在列上,最后将其结合得到(2D)2PCA,使其可以同时在行列工作
假设有原始矩阵$A\in\mathbb{R}^{m \times n }$,使用过程如下:
1.计算协方差矩阵
其中$A_k=[(A_k^{(1)})^{T} \ (A_k^{(2)})^{T} \ …\ (A_k^{(m)})^{T}]^{T},\overline{A}=[(\overline{A}^{(1)})^{T} \ (\overline{A}^{(2)})^{T} \ …\ (\overline{A}^{(m)})^{T}]^{T}, \ A_k^{(i)}, \overline{A}^{(i)}$表示$A_k,\overline{A}$的第$i$行
其中$A_k=[(A_k^{(1)}) \ (A_k^{(2)}) \ …\ (A_k^{(n)})],\overline{A}=[(\overline{A}^{(1)}) \ (\overline{A}^{(2)}) \ …\ (\overline{A}^{(n)})],A_k^{(j)},\overline{A}^{(j)}$表示$A_k,\overline{A}$的第$j$列
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列
4.实现数据降维
可以参考 https://blog.csdn.net/scott198510/article/details/76099700
1 | from sklearn.manifold import TSNE |
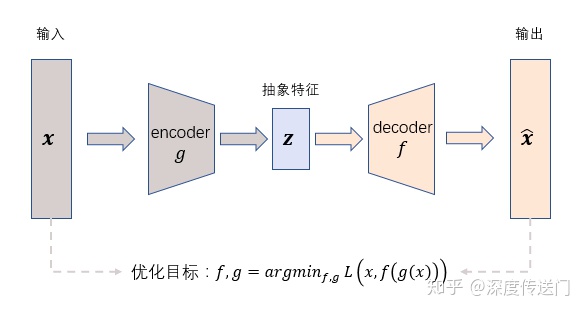
AutoEncoder在优化过程中无需使用样本的label,通过最小化重构误差希望学习到样本的抽象特征表示z,这种无监督的优化方式大大提升了模型的通用性。
是机器学习中对原始损失函数引入额外信息,以便防止过拟合和提高模型泛化性能的一类方法的统称。
L1正则化可以使得参数稀疏化,即得到的参数是一个稀疏矩阵,可以用于特征选择。
L1是每次减去一个常数的收敛,所以L1更容易收敛到0。
L2正则化使得参数平滑。
L2是每次乘上一个小于1的倍数进行收敛,所以L2使得参数平滑。
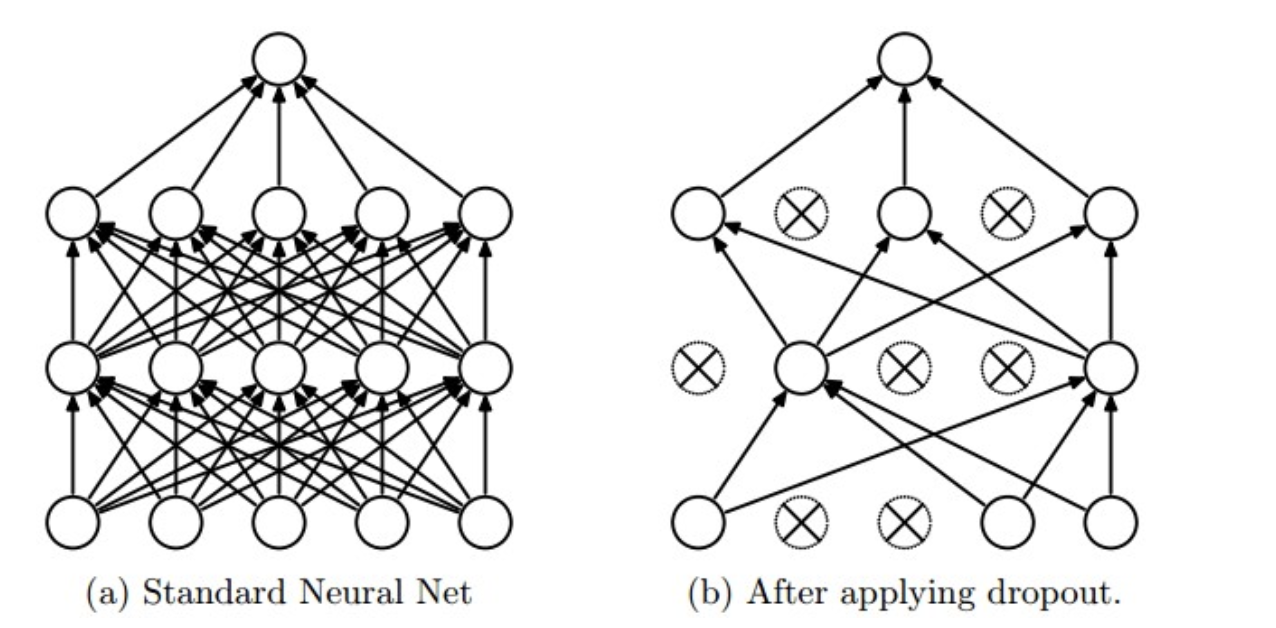
使用:在训练时,每个神经单元以概率$p$被保留(Dropout丢弃率为$1−p$);在预测阶段,每个神经单元都是存在的。
原理:神经网络通过Dropout层以一定比例随即的丢弃神经元,使得每次训练的网络模型都不相同,多个Epoch下来相当于训练了多个模型,同时每一个模型都参与了对最终结果的投票,从而提高了模型的泛化能力,类似bagging。
https://www.cnblogs.com/zingp/p/11631913.html
损失函数一般都要用可导函数,因为常用的优化算法,比如梯度下降,牛顿法,都需要导数。
https://zhuanlan.zhihu.com/p/100921909
SVM模型的损失函数本质上就是 Hinge Loss + L2 正则化