A Deep Look into Neural Ranking Models for Information Retrieval
https://par.nsf.gov/servlets/purl/10277191
3 A Unified Model Formulation
So a generalized LTR problem is to find the optimal ranking function f ∗ by minimizing the loss function over some labeled dataset
f 是ranking function,s是query,t是候选集,y is the label set where labels represent grades
Without loss of generality, the ranking function f could be further abstracted by the following unified formulation
ψ, ϕare representation functions which extract features from s and t respectively η is the interaction function which extracts features from (s, t) pair, and g is the evaluation function which computes the relevance score based on the feature representations.
4. Model Architecture
4.1. Symmetric vs. Asymmetric Architectures
Symmetric Architecture: The inputs s and t are assumed to be homogeneous, so that symmetric network structure could be applied over the inputs
Asymmetric Architecture: The inputs s and t are assumed to be heterogeneous, so that asymmetric network structures should be applied over the inputs
4.2. Representation-focused vs. Interaction-focused Architectures
Representation-focused Architecture: The underlying assumption of this type of architecture is that relevance depends on compositional meaning of the input texts. Therefore, models in this category usually define complex representation functions ϕ and ψ (i.e., deep neural networks), but no interaction function η
Interaction-focused Architecture: The underlying assumption of this type of architecture is that relevance is in essence about the relation between the input texts, so it would be more effective to directly learn from interactions rather than from individual representations. Models in this category thus define the interaction function η rather than the representation functions ϕ and ψ
Hybrid Architecture: In order to take advantage of both representation focused and interaction-focused architectures, a natural way is to adopt a hybrid architecture for feature learning. We find that there are two major hybrid strategies to integrate the two architectures, namely combined strategy and coupled strategy.
4.3. Single-granularity vs. Multi-granularity Architecture
Single-granularity Architecture: The underlying assumption of the single granularity architecture is that relevance can be evaluated based on the high level features extracted by ϕ, ψ and η from the single-form text inputs.
Multi-granularity Architecture: The underlying assumption of the multigranularity architecture is that relevance estimation requires multiple granularities of features, either from different-level feature abstraction or based on different types of language units of the inputs
5. Model Learning
5.1. Learning objective
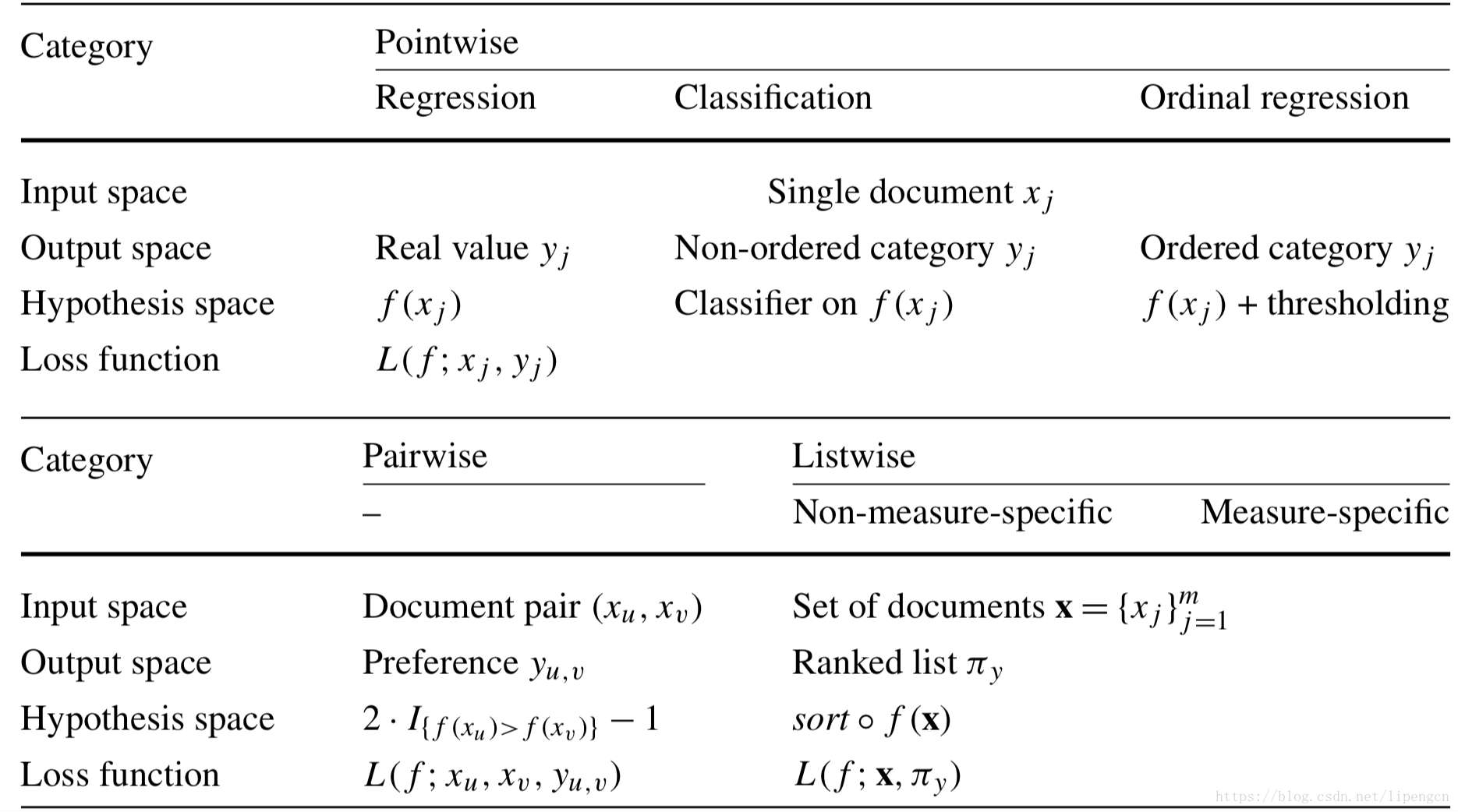
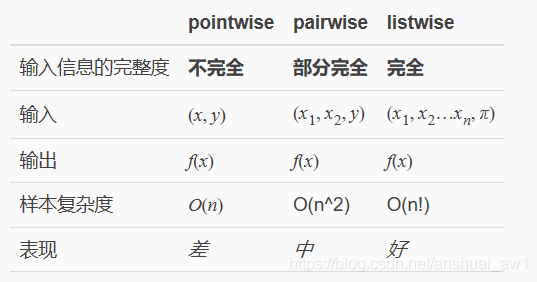
Similar to other LTR algorithms, the learning objective of neural ranking models can be broadly categorized into three groups: pointwise, pairwise, and listwise.
5.1.1. Pointwise Ranking Objective
1 loss
The idea of pointwise ranking objectives is to simplify a ranking problem to a set of classification or regression problems
a. Cross Entropy
For example, one of the most popular pointwise loss functions used in neural ranking models is Cross Entropy:
b. Mean Squared Error
There are other pointwise loss functions such as Mean Squared Error for numerical labels, but they are more commonly used in recommendation tasks.
2 优缺点
a.advantages
First, it simple and easy to scale. Second, the outputs have real meanings and value in practice. For instance, in sponsored search, a model learned with cross entropy loss and clickthrough rates can directly predict the probability of user clicks on search ads, which is more important than creating a good result list in some application scenarios.
b.disadvantages
less effective ,Because pointwise loss functions consider no document preference or order information, they do not guarantee to produce the best ranking list when the model loss reaches the global minimum.
5.1.2. Pairwise Ranking Objective
1 loss
Pairwise ranking objectives focus on optimizing the relative preferences between documents rather than their labels.
a.Hinge loss
b.cross entropy
RankNet
2 优缺点
a.advantages
effective in many tasks
b.disadvantages
pairwise methods does not always lead to the improvement of final ranking metrics due to two reasons: (1) it is impossible to develop a ranking model that can correctly predict document preferences in all cases; and (2) in the computation of most existing ranking metrics, not all document pairs are equally important.
5.1.3. Listwise Ranking Objective
1 loss
listwise loss functions compute ranking loss with each query and their candidate document list together
a. ListMLE
https://blog.csdn.net/qq_36478718/article/details/122598406
b.Attention Rank function
https://arxiv.org/abs/1804.05936
c. softmax-based listwise
https://arxiv.org/pdf/1811.04415.pdf
2 优缺点
a.advantages
While listwise ranking objectives are generally more effective than pairwise ranking objectives
b.disadvantages
their high computational cost often limits their applications. They are suitable for the re-ranking phase over a small set of candidate documents
5.1.4. Multi-task Learning Objective
the optimization of neural ranking models may include the learning of multiple ranking or non-ranking objectives at the same time.
5.2. Training Strategies
1 Supervised learning
2 Weakly supervised learning
3 Semi-supervised learning
6. Model Comparison
比较了常见模型在不同应用的效果
1 Ad-hoc Retrieval
https://blog.csdn.net/qq_44092699/article/details/106335971
Ad-hoc information retrieval refers to the task of returning information resources related to a user query formulated in natural language.
2 QA