The ListNet method grows on the bases of RankNet, they both employ the Cross Entropy function as a loss function and Gradient Descendant as algorithm to train a Neural Network Model. While the ListNet uses document list as instances, RankNet uses document pairs.

We investigated why the listwise method ListNet can outperform the pairwise methods of RankNet, Ranking SVM, and RankBoost.

https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2007-40.pdf

1.for the pairwise approach the number of document pairs varies largely from query to query

2.The pairwise approach actually employs a ‘pairwise’ loss function, which might be too loose as an approximation of the performance measures

https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2007-40.pdf

https://blog.csdn.net/Mr_tyting/article/details/80554849

核心思想为：

1. Given two lists of scores（模型和人）
2. we can first calculate two permutation probability distributions from them（简化到用top1）
3. and then calculate the distance between the two distributions as the listwise loss function.（交叉熵）

4. Probability Models

4.1. Permutation Probability

$\pi=(2,3,1) $指的是对象2排在第一位

上面是topn的形式

因为总共有n！次排序组合

4.2. Top One Probability

topk：

$$P_s(\pi)=\prod \limits_{j=1}^K\frac{\phi(S_{\pi(j)})}{\sum_{k=j}^n\phi(S_{\pi(k)})}$$

总共有N ! / ( N − k ) ! 种不同排列，大大减少了计算复杂度

top1：

此时有n种不同排列情况

概率分布的含义：对于每个j，分别都处于第一的概率是多少

5.Learning Method: ListNet

We employ a new learning method for optimizing the listwise loss function based on top one probability, with Neural Network as model and Gradient Descent as optimization algorithm. We refer to the method as ListNet.

$y^{(i)}$是真实的score list，有个疑问就是$y^{(i)}$怎么得到？关于这个，应该是先有真实的score list（人打），然后基于score list得到排序，参考 https://zhuanlan.zhihu.com/p/66514492

核心步骤

1.打标得到真实的score list，模型得到预测的score list

2.然后用softmax得到真实的和预测的score list的概率分布

3.然后用交叉熵计算两种概率分布的差距

博客

https://zhuanlan.zhihu.com/p/66514492

Listwise Approach to Learning to Rank - Theory and Algorithm（ListMLE）

http://icml2008.cs.helsinki.fi/papers/167.pdf

Learning to Rank: From Pairwise Approach to Listwise Approach（ListNet）

https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2007-40.pdf

1.RankNet

RankNet采用pairwise的方法进行模型训练。

loss推导

给定特定$query$下的两个文档$U_i$和$U_j$，其特征向量分别为$x_i$和$x_j$，经过RankNet进行前向计算得到对应的分数为$s_i=f(x_i)$和$s_j=f(x_j)$。用$U_i \rhd U_j$表示$U_i$比$U_j$排序更靠前。继而可以用下面的公式来表示$U_i$应该比$U_j$排序更靠前的概率：

$$P_{ij} \equiv P(U_i \rhd U_j) \equiv \frac{1}{1+e^{-\sigma(s_i-s_j)}}$$

定义$S_{ij} \in \{0,\pm1\}$为文档$i$和文档$j$被标记的标签之间的关联，即

$$S_{ij}=\left\{ \begin{aligned} 1&& 文档i比文档j更相关\\ 0&& 文档i和文档j相关性一致\\ -1&& 文档j比文档i更相关 \end{aligned} \right.$$

定义$\overline{P}_{ij}=\frac{1}{2}(1+S_{ij})$表示$U_i$应该比$U_j$排序更靠前的已知概率，则可以用交叉熵定义优化目标的损失函数：

$$\begin{align*} C&=-\overline{P}_{ij}log{P_{ij}}-(1-\overline{P}_{ij})log(1-P_{ij}) \\&=\frac{1}{2}(1-S_{ij})\sigma(s_i-s_j)+log(1+e^{-\sigma(s_i-s_j)}) \end{align*}$$

注意：$\sigma$是超参数

ranknet 加速

2.LambdaRank

ranket缺陷为只考虑pair的相对位置没有考虑二者在列表的整体位置

LambdaRank本质为ranknet基础上加入Listwise的指标，因此有人将LambdaRank归为listwise方法，也有归到pairwise方法

2.1 RankNet的局限

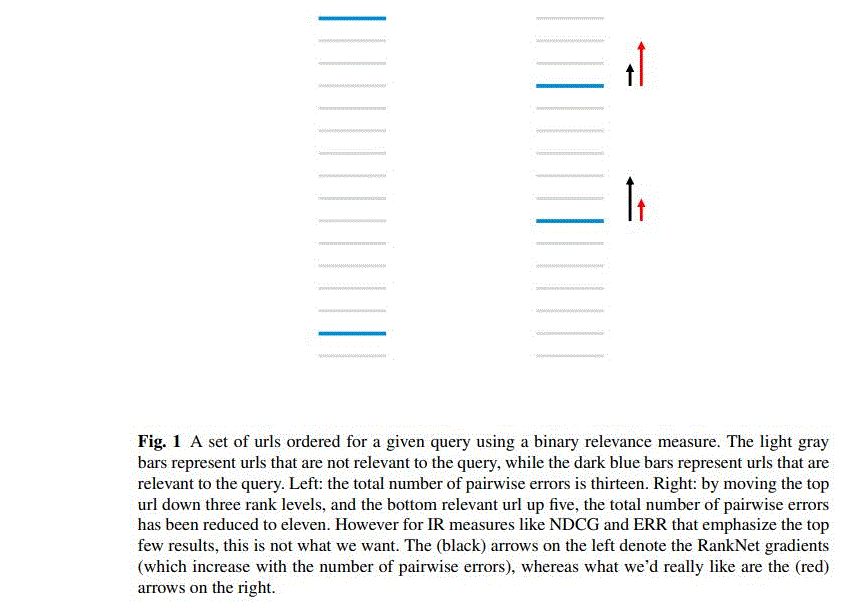
2.2 LambdaRank定义

$$\begin{align*} \frac{\partial{C}}{\partial{w_k}}&=\frac{\partial{C}}{\partial{s_i}}\frac{\partial{s_i}}{\partial{w_k}}+\frac{\partial{C}}{\partial{s_j}}\frac{\partial{s_j}}{\partial{w_k}} \\&=\sigma\left(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}\right)\left(\frac{\partial{s_i}}{\partial{w_k}}-\frac{\partial{s_j}}{\partial{w_k}}\right) \\&=\lambda_{ij}\left(\frac{\partial{s_i}}{\partial{w_k}}-\frac{\partial{s_j}}{\partial{w_k}}\right) \end{align*} \\其中\lambda_{ij}=\frac{\partial{C}}{\partial{s_i}}=-\frac{\partial{C}}{\partial{s_j}}=\sigma\left(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}\right)$$

上述公式可以进一步简化，即只考虑$S_{ij}=1$ （为什么可以？？？？？）

那么Lambda，$\lambda$，就是梯度

$$\lambda_{ij}=\frac{-\sigma}{1+e^{\sigma(s_i-s_j)}}$$

为了加强排序中前后顺序的重要性，Lambda在原基础上引入评价指标Z（如NDCG），把交换两个文档的位置引起的评价指标的变化$|\Delta Z_{ij}|$作为其中一个因子：

$$\lambda_{ij}=\frac{\partial{C}}{\partial{s_i}}=\frac{-\sigma}{1+e^{\sigma(s_i-s_j)}}|\Delta Z_{ij}|$$

反推出 LambdaRank 的损失函数：

$$C=log(1+e^{\sigma (s_i-s_j)})|\Delta Z_{ij}|$$

3.LambdaMART

属于listwise，也有说pairwise。

LambdaMART=lambda($\lambda$)+mart(gbdt)

$\lambda$就是梯度，lambdarank就是一种loss，gbdt就是模型

lambdamart说白了就是利用gbdt计算lambdarank中s，或者说将lambdarank作为gbdt的loss

gbdt，lambdamart算法流程差异在于step1

GBDT：

1. 初始化： $f_0(x) = \mathop{\arg\min}\limits_\gamma \sum\limits_{i=1}^N L(y_i, \gamma)$
2. for m=1 to M:
   (a). 计算负梯度： $\tilde{y}_i = -\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, \qquad i = 1,2 \cdots N$
   (b). $\left \{ R_{jm} \right\}_1^J = \mathop{\arg\min}\limits_{\left \{ R_{jm} \right\}_1^J}\sum\limits_{i=1}^N \left [\tilde{y}_i - h_m(x_i\,;\,\left \{R_{jm},b_{jm} \right\}_1^J) \right]^2$
   (c). $\gamma_{jm} = \mathop{\arg\min}\limits_\gamma \sum\limits_{x_i \in R_{jm}}L(y_i,f_{m-1}(x_i)+\gamma)$
   (d). $f_m(x) = f_{m-1}(x) + \sum\limits_{j=1}^J \gamma_{jm}I(x \in R_{jm})$
3. 输出$f_M(x)$

LambdaMART:

参考

https://blog.csdn.net/laolu1573/article/details/87372514

https://liam.page/uploads/slides/lambdamart.pdf

https://blog.csdn.net/zpalyq110/article/details/79527653

https://zhuanlan.zhihu.com/p/86354141

https://www.cnblogs.com/genyuan/p/9788294.html

https://blog.csdn.net/huagong_adu/article/details/40710305

https://zhuanlan.zhihu.com/p/270608987

https://www.cnblogs.com/bentuwuying/p/6690836.html

paper原文： https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/MSR-TR-2010-82.pdf

https://www.jianshu.com/p/a78b3f52c221

https://blog.csdn.net/zhoujialin/article/details/46697409

https://blog.csdn.net/w28971023/article/details/45849659

https://zhuanlan.zhihu.com/p/270608987