2021-09-15 0d9efcf05de62def8a88e43181dbe72e 99+ fast 0.0 k

RNN总结

1.单元

1.1 普通RNN单元

1.2 LSTM

1.3 GRU

2.结构

1.1 输入、输出

1.2 是否双向

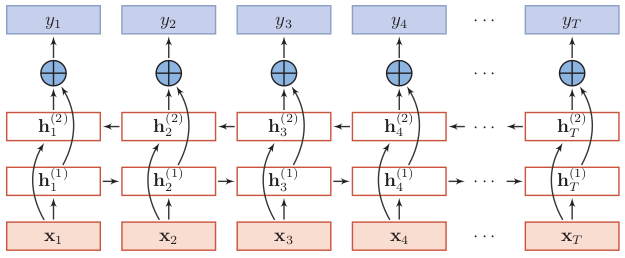
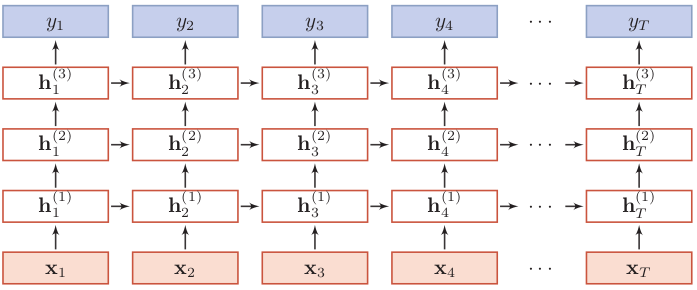
1.3 是否堆叠

参考

https://blog.csdn.net/gaohanjie123/article/details/88699664

https://www.cnblogs.com/Luv-GEM/p/10788849.html

NLP 特征提取器

RNN

2021-09-15 607add707f93360424dff10eb802fe91 99+ 2 m 0.3 k

RoBERTa A Robustly Optimized BERT Pretraining Approach

1.和BERT比较

在结构上和原版BERT没有差异，主要的改动在于：

2.改动分析

2.1 Static vs. Dynamic Masking

static masking: 原本的BERT采用的是static mask的方式，就是在create pretraining data中，先对数据进行提前的mask

dynamic masking: 每一次将训练example喂给模型的时候，才进行随机mask。

结果对比：

结论：动态占优

2.2 Model Input Format and Next Sentence Prediction

做了结果对比试验，结果如下：

结论：

Model Input Format:

1.find that using individual sentences hurts performance on downstream tasks

Next Sentence Prediction:

1.removing the NSP loss matches or slightly improves downstream task performance

2.3 Training with large batches

2.4 Text Encoding

采用BBPE而不是wordpiece

3 常见问题

1 roberta tokenizer 没有token_type_ids？
roberta 取消了NSP，所以不需要segment embedding 也就不需要token_type_ids，但是使用的时候发现中文是有token_type_ids的，英文没有token_type_ids的。没有token_type_ids，两句话怎么区别，分隔符sep还是有的，只是没有segment embedding

2 使用避坑

https://blog.csdn.net/zwqjoy/article/details/107533184

https://hub.fastgit.org/ymcui/Chinese-BERT-wwm

参考

https://zhuanlan.zhihu.com/p/103205929

https://zhuanlan.zhihu.com/p/143064748

https://blog.csdn.net/zwqjoy/article/details/107533184

https://hub.fastgit.org/ymcui/Chinese-BERT-wwm

NLP PTM

PTM

2021-09-10 11a71155e1e45a0951c7148ccf224020 99+ 2 m 0.4 k

python环境

1.包

1.1 下载包

下载源有官方源，阿里源，豆瓣源，清华源等

1 离线下载

去有网的环境下载包，然后去没有的环境安装

1.网页下

不能下载依赖包

2.命令行下载

可以下载依赖包

pip download -d 文件夹 packagename

pip download -d 文件夹 -r requirements.txt

2 在线下载

pip

1.更换pip源

修改文件

1	vim ~/.pip/pip.conf # 没有就创建一个，在 ~/.pip/下

增加内容

[global]
index-url=https://pypi.tuna.tsinghua.edu.cn/simple
# index-url=http://pypi.douban.com/simple/
[install]
trusted-host=pypi.tuna.tsinghua.edu.cn

2.查看路径

which python, which pip

3.安装指定python版本的包

pythonversion -m pip

4.指定下载源

pip install -i XXX

1.2 使用包

import

绝对路径：从工程的最外层开始

相对路径：利用.（同级）和..（上级）

怎么添加包的搜路径

https://blog.csdn.net/weixin_40449300/article/details/79327201

2.虚拟环境

1.anaconda

1.修改环境变量

1.vim ~/.bashrc

2.添加如下内容

export PYTHON_HOME=/usr/local/anaconda3/bin

export PATH=$PYTHON_HOME:$PATH

3.source ~/.bashrc

2.修改conda源

vim ~/.condarc

3.文件结构

envXXX/(bin lib )

包在lib/pythonXX/site-packages

2.virtualenv

https://blog.csdn.net/weixin_44015669/article/details/115666912#Ej3Q4

/usr/bin/python3.7 -m venv mypython

source mypython/bin/acticate

deactivate

3.环境迁移

1.pip

1 切到有网环境

环境1

pip freeze > requirements.txt

环境2

pip install -r requirements.txt

2 切到没有网环境

环境1

pip freeze > requirements.txt

pip download -d 文件夹 -r requirements.txt

环境2

pip install -r requirements.txt —no-index —find-links 文件夹

2.conda

conda pack

3.直接拷贝anaconda某个env

python

python环境

2021-09-08 0eb98971f8b7965b646875b43430b474 99+ 6 m 1.0 k

降维

1.意义

1.高纬空间样本具有稀疏性，容易欠拟合

2.可视化

3.维度过大导致训练时间长，预测慢

2.分类

大致分为线形降维度和非线性降维，线形降维包括PCA，LDA等，非线性降维包括LLE，t-SNE，auto encoder等。

3.PCA系列

3.1 PCA

假设矩阵$x\in \mathbb{R}^{ n}$，假设有$M$个样本，将原始数据按列组成$M$ 行$ n $列矩阵$ X\in \mathbb{R}^{M\times n}$，PCA的使用过程为：

1.计算协方差矩阵$G_t \in \mathbb{R}^{n \times n}$

$G_t=\frac{1}{M}\sum_{j=1}^{M}(X-\overline{X})^T(X-\overline{X})$

注意，其中$\overline{X}\in \mathbb{R}^{n}$为列的均值，$X-\overline{X}$表示将$ X$ 的每一列进行零均值化，即减去这一列的均值

2.求出协方差矩阵的特征值及对应的特征向量

$(U,\sum,V)=SVD(G_t)$

3.将特征向量按对应的特征值大小排列，取前 $k$ 列组成矩阵 $P\in \mathbb{R}^{n \times k} $

$P=U(:,1:k)$

4.实现数据降维

$y_{[1\times k]}=x_{[1\times n ]}P_{[n\times k]}$

局限：

a. PCA只能针对1D的向量，对于2D的矩阵而言，比如图片数据，需要先flatten成向量

3.2 2DPCA

将2D的矩阵flatten成向量其实丢失了行列的位置信息，为了直接在2D的矩阵上实现降维，提出了2DPCA。

假设有原始矩阵$A\in\mathbb{R}^{m \times n }$，使用过程如下：

1.计算协方差矩阵

$G_t=\frac{1}{M}\sum_{j=1}^{M}(A_j-\overline{A})^{T}(A_j-\overline{A}) \\\overline{A}=\frac{1}{M}\sum_{j=1}^{M}A_j$

2.求出协方差矩阵的特征值及对应的特征向量

$(U,\sum,V)=SVD(G_t)$

3.将特征向量按对应的特征值大小排列，取前 $k$ 列组成矩阵

$X=U(:,1:k)$

4.实现数据降维

$Y_{[m\times k]}=A_{[m\times n ]}X_{[n\times k]}$

3.3 （2D）2PCA

作者证明了2DPCA只是在行上工作，然后提出了Alternative 2DPCA可以工作在列上，最后将其结合得到（2D）2PCA，使其可以同时在行列工作

假设有原始矩阵$A\in\mathbb{R}^{m \times n }$，使用过程如下：

1.计算协方差矩阵

$G_x=\frac{1}{M}\sum_{k=1}^{M}\sum_{i=1}^{m}(A_k^{(i)}-\overline{A}^{(i)})^{T}(A_k^{(i)}-\overline{A}^{(i)})$

其中$A_k=[(A_k^{(1)})^{T} \ (A_k^{(2)})^{T} \ …\ (A_k^{(m)})^{T}]^{T},\overline{A}=[(\overline{A}^{(1)})^{T} \ (\overline{A}^{(2)})^{T} \ …\ (\overline{A}^{(m)})^{T}]^{T}, \ A_k^{(i)}, \overline{A}^{(i)}$表示$A_k,\overline{A}$的第$i$行

$\\G_z=\frac{1}{M}\sum_{k=1}^{M}\sum_{j=1}^{n}(A_k^{(j)}-\overline{A}^{(j)})(A_k^{(j)}-\overline{A}^{(j)})^{T}$

其中$A_k=[(A_k^{(1)}) \ (A_k^{(2)}) \ …\ (A_k^{(n)})],\overline{A}=[(\overline{A}^{(1)}) \ (\overline{A}^{(2)}) \ …\ (\overline{A}^{(n)})],A_k^{(j)},\overline{A}^{(j)}$表示$A_k,\overline{A}$的第$j$列

2.求出协方差矩阵的特征值及对应的特征向量

$(U_x,\sum x,V_x)=SVD(G_x) \\(U_z,\sum z,V_z)=SVD(G_z)$

3.将特征向量按对应的特征值大小排列

$X=U_x(:,1:k) \in \mathbb{R}^{n\times k} \\Z=U_z(:,1:q) \in \mathbb{R}^{m\times q}$

4.实现数据降维

$C_{[q\times k]}=Z^{T}_{[q\times m]}A_{[m\times n ]}X_{[n\times k]}$

4.t-SNE

4.1 原理

可以参考 https://blog.csdn.net/scott198510/article/details/76099700

4.2代码

from sklearn.manifold import TSNE
from matplotlib import pylab
import  torch
import  pandas as pd


embdding=torch.load(path1)
words = pd.read_csv(path2)

words_embedded = TSNE(n_components=2).fit_transform(embdding)

pylab.figure(figsize=(20, 20))
for i, label in enumerate(words):
  x, y = words_embedded[i, :]
  pylab.scatter(x, y)
  pylab.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points',
                 ha='right', va='bottom')
pylab.show()

5.auto encoder

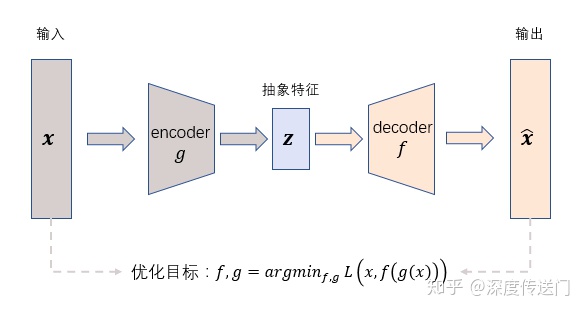
AutoEncoder在优化过程中无需使用样本的label，通过最小化重构误差希望学习到样本的抽象特征表示z，这种无监督的优化方式大大提升了模型的通用性。

参考

https://zhuanlan.zhihu.com/p/68903857

https://blog.csdn.net/scott198510/article/details/76099700

机器学习模型结构

降维

2021-09-07 a163153037c01b910d58c60152e6ada9 99+ 3 m 0.5 k

正则化

是机器学习中对原始损失函数引入额外信息，以便防止过拟合和提高模型泛化性能的一类方法的统称。

1.L1正则（Lasso回归）

L1正则化可以使得参数稀疏化，即得到的参数是一个稀疏矩阵，可以用于特征选择。

$\begin{align*} L_{L1}(w)&=L(w)+\lambda\Vert w \Vert_1=L(w)+\lambda\sum_{i=1}^{N}|w_i| \\ \frac{\partial L_{L1}}{\partial w_i}&=\frac{\partial L}{\partial w_i}+\lambda \ sgn(w_i) \\w_i &\rightarrow w_i-\eta(\frac{\partial L}{\partial w_i}+\lambda \ sgn(w_i)) \rightarrow w_i-\eta\lambda \ sgn(w_i)-\eta\frac{\partial L}{\partial w_i} \end{align*}$

L1是每次减去一个常数的收敛，所以L1更容易收敛到0。

2.L2正则（Ridge回归）

L2正则化使得参数平滑。

$\begin{align*} L_{L2}(w)&=L(w)+\lambda\Vert w \Vert_2^2=L(w)+\lambda\sum_{i=1}^{N}w_i^2 \\ \frac{\partial L_{L2}}{\partial w_i}&=\frac{\partial L}{\partial w_i}+2\lambda w_i \\w_i& \rightarrow w_i-\eta(\frac{\partial L}{\partial w_i}+2\lambda w_i) \rightarrow(1-2\eta\lambda)w_i-\eta \frac{\partial L}{\partial w_i} \end{align*}$

L2是每次乘上一个小于1的倍数进行收敛，所以L2使得参数平滑。

3.dropout

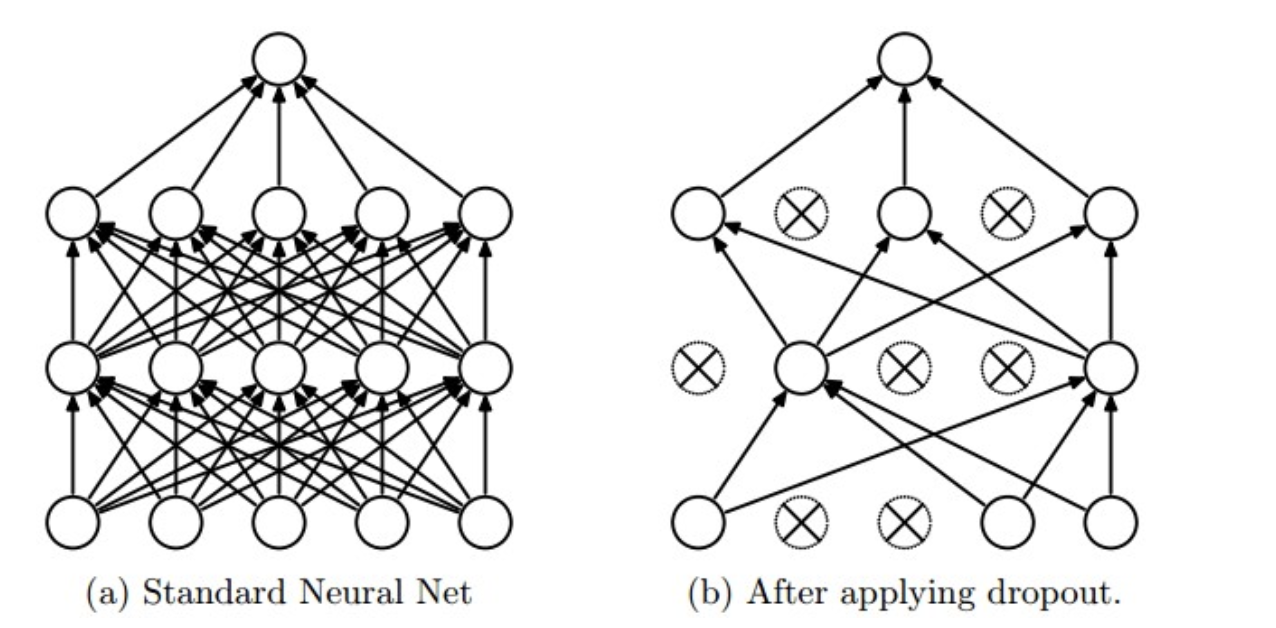
使用：在训练时，每个神经单元以概率$p$被保留(Dropout丢弃率为$1−p$)；在预测阶段，每个神经单元都是存在的。

原理：神经网络通过Dropout层以一定比例随即的丢弃神经元，使得每次训练的网络模型都不相同，多个Epoch下来相当于训练了多个模型，同时每一个模型都参与了对最终结果的投票，从而提高了模型的泛化能力，类似bagging。

参考

https://www.cnblogs.com/zingp/p/11631913.html

https://blog.csdn.net/b876144622/article/details/81276818

https://www.zhihu.com/question/37096933/answer/70494622

机器学习训练技巧

正则化

2021-09-07 a1181f0da285c1067e9bf5d83c659fb8 99+ a minute 0.2 k

损失函数

损失函数一般都要用可导函数，因为常用的优化算法，比如梯度下降，牛顿法，都需要导数。

1.回归损失

1.1 Mean Squared Error

$L=\frac{1}{N}\sum_{i=1}^{N}(y_i-\hat{y}_i)^2$

1.2 Mean Absolute Error

$L=\frac{1}{N}\sum_{i=1}^{N}|y_i-\hat{y}_i|$

1.3 Huber Loss ( Smooth Mean Absolute Error Loss )

$L=\frac{1}{N}\sum_{i=1}^{N}[\mathbb{1}_{|y_i-\hat{y_i}|\le \delta}\frac{(y_i-\hat{y_i})^2}{2}+\mathbb{1}_{|y_i-\hat{y_i}|> \delta} \ (\delta \cdot |y_i-\hat{y_i}|-\frac{1}{2}\delta^{2})]$

2.分类损失

2.1 Cross-entropy loss

https://zhuanlan.zhihu.com/p/100921909

K是种类数量
y是标签
p是神经网络的输出，也就是指类别是i的概率

2.2 Hinge loss

$L=max(0,1-y\cdot \hat{y})$

SVM模型的损失函数本质上就是 Hinge Loss + L2 正则化

参考

https://blog.csdn.net/m0_38007695/article/details/114983574

机器学习 loss

损失函数

2021-09-06 64d7930bfb2e268ead146758905948c7 99+ a minute 0.1 k

集成学习

目前常见的集成学习可以分类为：1.Bagging 2.Boosting 3.Stacking 4.Blending

1.Bagging

bagging是解决variance问题。

2.Boosting

boosting是解决bias问题。

Bagging，Boosting二者之间的区别

https://zhuanlan.zhihu.com/p/81340270

3.Stacking

stacking和boosting的最大区别在于：boosting的基学习器是一个，stacking的基学习器是多个

4.Blending

和stacking区别： https://www.jianshu.com/p/4380cd1def76

参考

https://zhuanlan.zhihu.com/p/105038453

https://zhuanlan.zhihu.com/p/126968534

https://blog.csdn.net/starter_____/article/details/79328749

集成学习集成学习

集成学习

2021-09-06 f6ec69d796f91514753f8400f57d4439 99+ 4 m 0.5 k

常见激活函数

作用：激活函数是来向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线

1.sigmoid

$\begin{align*} y&=\frac{1}{1+e^{-x}} \\y^{'}&=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})=y(1-y) \end{align*}$

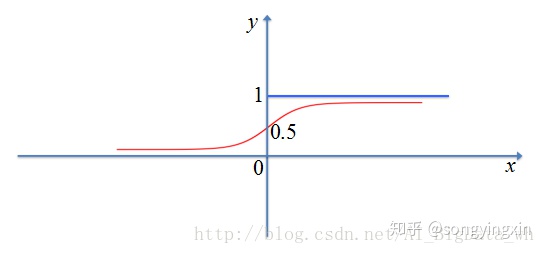
一般应用在二分类的输出层

缺点：

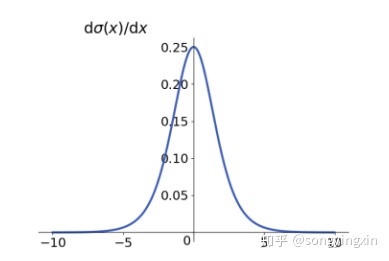
1.sigmoid 极容易导致梯度消失问题，可以从导数曲线可以看出，绝大多数的导数值为0

2.Sigmoid 函数的输出不是以零为中心的（non-zero-centered），这会导致神经网络收敛较慢，详细原因请参考 https://liam.page/2018/04/17/zero-centered-active-function/

2.softmax

$S_i=\frac{e^i}{\sum_je^j}$

和sigmoid关系：Softmax函数是二分类函数Sigmoid在多分类上的推广

https://zhuanlan.zhihu.com/p/356976844

3.tanh

$\begin{align*} y&=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \\y^{'}&=1-(tanh(x))^{2} \end{align*}$

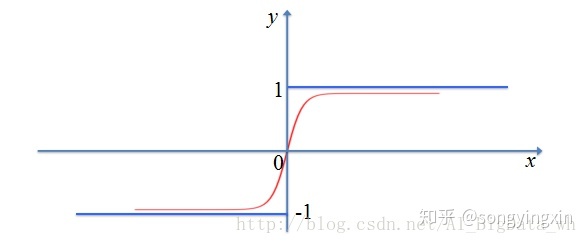
优点:

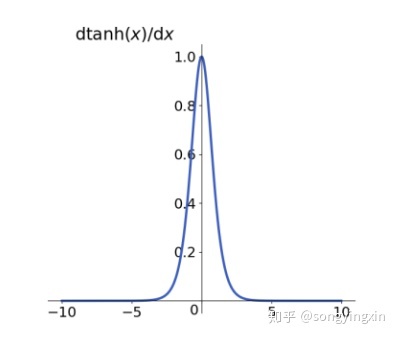
1.tanh解决了sigmoid中的 zero-centered 问题

缺点：

2.对于梯度消失问题依旧无能为力。

4.Relu系列

4.1 Relu

$\begin{align*} y&=max(0,x) \\ y^{'}&=\left\{ \begin{array}{cl} 1 & \ x \ge 0 \\ 0 & \ x < 0 \\ \end{array} \right. \end{align*}$

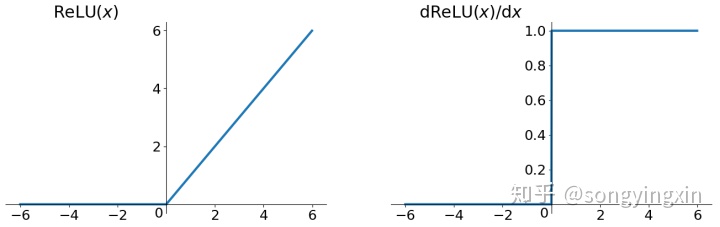
优点:

1.可以缓解梯度消失，因为导数在正数部分是恒等于1的

缺点：

1.Relu的输出不是zero-centered

2.由于负数部分导数恒为0，会导致一些神经元无法激活，叫做Dead ReLU Problem

4.2 leaky Relu

leaky Relu就是为了解决Relu的0区间带来的影响，其数学表达为：

$\begin{align*} y&=\left\{ \begin{array}{cl} x & \ x \ge 0 \\ kx & \ x < 0 \\ \end{array} \right. \\ y^{'}&=\left\{ \begin{array}{cl} 1 & \ x \ge 0 \\ k & \ x < 0 \\ \end{array} \right. \end{align*}$

其中$k$是为超参数，一般数值较小，比如0.01

4.3 Elu

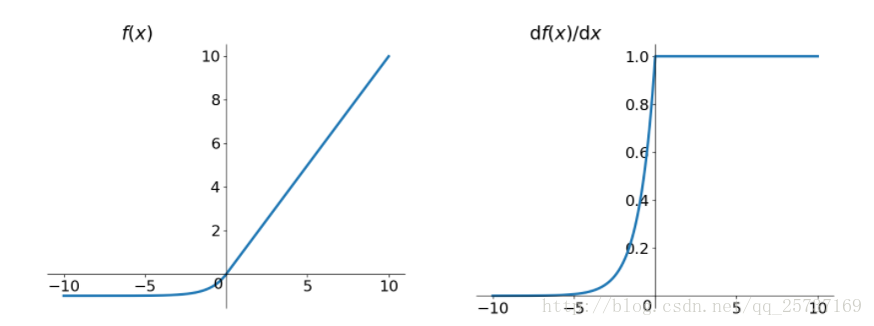
Elu激活函数也是为了解决Relu的0区间带来的影响，其数学表达为：

$\begin{align*} y&=\left\{ \begin{array}{cl} x & \ x \ge 0 \\ \alpha(e^{x}-1) & \ x < 0 \\ \end{array} \right. \\ y^{'}&=\left\{ \begin{array}{cl} 1 & \ x \ge 0 \\ \alpha e^{x} & \ x < 0 \\ \end{array} \right. \end{align*}$

Elu相对于leaky Relu来说，计算要更耗时间一些

参考

https://zhuanlan.zhihu.com/p/44398148

https://liam.page/2018/04/17/zero-centered-active-function/

https://www.cnblogs.com/tornadomeet/p/3428843.html

https://www.cnblogs.com/chamie/p/8665251.html

https://zhuanlan.zhihu.com/p/33006526?from_voters_page=true

机器学习模型结构

激活函数

2021-09-04 1f189f8e824cf01149d323b5bd5e3584 99+ 3 m 0.4 k

过拟合，欠拟合以及解决办法

1.偏差和方差

$\overline{f}(\textbf{x})=\mathbb{E}_D[f(\textbf{x};D)]$

a.偏差

期望输出与真实标记的差别称为偏差（bias），即

$bias^{2}(\textbf{x})=(\overline{f}(\textbf{x})-y)^{2}$

b.方差

$var(\textbf{x})=\mathbb{E}_D[(f(\textbf{x};D)-\overline{f}(x))^2]$

c.噪声

$\xi^{2}=\mathbb{E}_D[(y_D-y)^2]$

d.泛化误差（error）

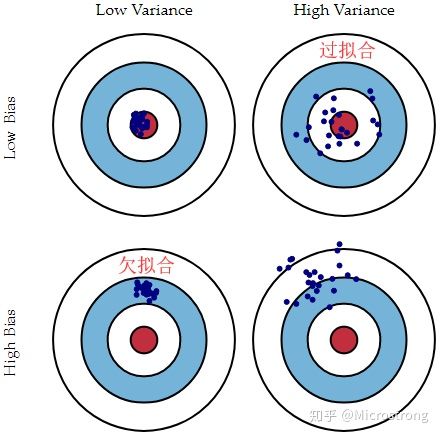
$\begin{align*} error&=\mathbb{E}_D[(f(\textbf{x};D)-y_D)^2] \\&=... \\&=(\overline{f}(\textbf{x})-y)^{2}+\mathbb{E}_D[(f(\textbf{x};D)-\overline{f}(x))^2]+\mathbb{E}_D[(y_D-y)^2] \\&=bias^{2}(\textbf{x})+var(\textbf{x})+\xi^{2} \end{align*}$

2.过拟合、欠拟合与偏差、方差的关系

欠拟合：模型不能适配训练样本，有一个很大的偏差。

过拟合：模型很好的适配训练样本，但在测试集上表现很糟，有一个很大的方差。

3.如何解决过拟合和欠拟合

a.模型能力（一个模型参数数量不同，不同模型）

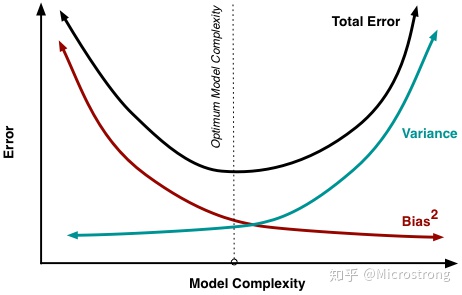
b.正则化

正则化参数出现的目的其实是防止过拟合情形的出现；如果我们的模型已经出现了欠拟合的情形，就可以通过减少正则化参数来消除欠拟合

c.特征数量

欠拟合：增加特征项

过拟合：减少特征项

d、训练的数据量

欠拟合：减少数据量

过拟合：增加数据量

参考

https://zhuanlan.zhihu.com/p/38853908

https://blog.csdn.net/hurry0808/article/details/78148756

https://blog.csdn.net/cltcj/article/details/119155683

机器学习训练技巧

过拟合、欠拟合

2021-09-04 5a6e62f83c4052377fc6d3f509682b43 99+ a minute 0.2 k

数据不平衡如何解决

1.基于数据

a.过采样和欠采样

对少数数据进行有放回的过采样，使原本的数据变的均衡，这样就是对少数数据进行了复制，容易造成过拟合。

对多数数据进行有放回/无放回的欠采样，这样会丢失一些样本，损失信息，模型只学会整体模式的一部分，容易欠拟合。

b.SMOTE算法

c.数据增强

通过人为或算法增加少数数据的数量

2.基于loss

使用代价函数时，可以增加小类样本的权值，降低大类样本的权值

参考

https://zhuanlan.zhihu.com/p/62877337

https://blog.csdn.net/asialee_bird/article/details/83714612

机器学习数据构造

数据不平衡

1.单元

1.1 普通RNN单元

1.2 LSTM

1.3 GRU

2.结构

1.1 输入、输出

1.2 是否双向

1.3 是否堆叠

参考

1.和BERT比较

2.改动分析

2.1 Static vs. Dynamic Masking

2.2 Model Input Format and Next Sentence Prediction

2.3 Training with large batches

2.4 Text Encoding

3 常见问题

参考

1.包

1.1 下载包

1 离线下载

2 在线下载

pip

1.2 使用包

2.虚拟环境

1.anaconda

2.virtualenv

3.环境迁移

1.意义

2.分类

3.PCA系列

3.1 PCA

3.2 2DPCA

3.3 （2D）2PCA

4.t-SNE

4.1 原理

4.2代码

5.auto encoder

参考

1.L1正则（Lasso回归）

2.L2正则（Ridge回归）

3.dropout

参考

1.回归损失

1.1 Mean Squared Error

1.2 Mean Absolute Error

1.3 Huber Loss ( Smooth Mean Absolute Error Loss )

2.分类损失

2.1 Cross-entropy loss

2.2 Hinge loss

参考

1.Bagging

2.Boosting

3.Stacking

4.Blending

参考

1.sigmoid

2.softmax

3.tanh

4.Relu系列

4.1 Relu

4.2 leaky Relu

4.3 Elu

参考

1.偏差和方差

2.过拟合、欠拟合与偏差、方差的关系

3.如何解决过拟合和欠拟合

参考

1.基于数据

2.基于loss

参考

Recents

Categories

Archives

Tags

Subscribe for updates