降维
1.意义
1.高纬空间样本具有稀疏性,容易欠拟合
2.可视化
3.维度过大导致训练时间长,预测慢
2.分类
大致分为线形降维度和非线性降维,线形降维包括PCA,LDA等,非线性降维包括LLE,t-SNE,auto encoder等。
3.PCA系列
3.1 PCA
假设矩阵$x\in \mathbb{R}^{ n}$,假设有$M$个样本,将原始数据按列组成$M$ 行$ n $列矩阵$ X\in \mathbb{R}^{M\times n}$,PCA的使用过程为:
1.计算协方差矩阵$G_t \in \mathbb{R}^{n \times n}$
注意,其中$\overline{X}\in \mathbb{R}^{n}$为列的均值,$X-\overline{X}$表示将$ X$ 的每一列进行零均值化,即减去这一列的均值
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列,取前 $k$ 列组成矩阵 $P\in \mathbb{R}^{n \times k} $
4.实现数据降维
局限:
a. PCA只能针对1D的向量,对于2D的矩阵而言,比如图片数据,需要先flatten成向量
3.2 2DPCA
将2D的矩阵flatten成向量其实丢失了行列的位置信息,为了直接在2D的矩阵上实现降维,提出了2DPCA。
假设有原始矩阵$A\in\mathbb{R}^{m \times n }$,使用过程如下:
1.计算协方差矩阵
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列,取前 $k$ 列组成矩阵
4.实现数据降维
3.3 (2D)2PCA
作者证明了2DPCA只是在行上工作,然后提出了Alternative 2DPCA可以工作在列上,最后将其结合得到(2D)2PCA,使其可以同时在行列工作
假设有原始矩阵$A\in\mathbb{R}^{m \times n }$,使用过程如下:
1.计算协方差矩阵
其中$A_k=[(A_k^{(1)})^{T} \ (A_k^{(2)})^{T} \ …\ (A_k^{(m)})^{T}]^{T},\overline{A}=[(\overline{A}^{(1)})^{T} \ (\overline{A}^{(2)})^{T} \ …\ (\overline{A}^{(m)})^{T}]^{T}, \ A_k^{(i)}, \overline{A}^{(i)}$表示$A_k,\overline{A}$的第$i$行
其中$A_k=[(A_k^{(1)}) \ (A_k^{(2)}) \ …\ (A_k^{(n)})],\overline{A}=[(\overline{A}^{(1)}) \ (\overline{A}^{(2)}) \ …\ (\overline{A}^{(n)})],A_k^{(j)},\overline{A}^{(j)}$表示$A_k,\overline{A}$的第$j$列
2.求出协方差矩阵的特征值及对应的特征向量
3.将特征向量按对应的特征值大小排列
4.实现数据降维
4.t-SNE
4.1 原理
可以参考 https://blog.csdn.net/scott198510/article/details/76099700
4.2代码
1 | from sklearn.manifold import TSNE |
5.auto encoder
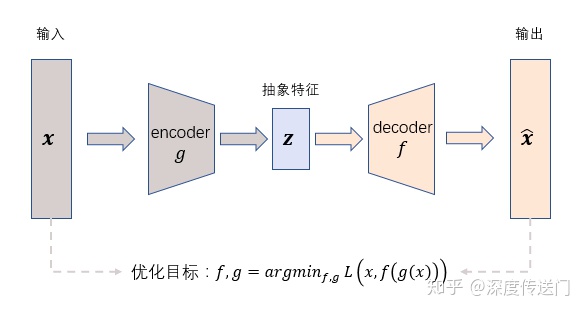
AutoEncoder在优化过程中无需使用样本的label,通过最小化重构误差希望学习到样本的抽象特征表示z,这种无监督的优化方式大大提升了模型的通用性。