KNN

KNN可以用来分类和回归，以分类为例。

一.算法流程

KNN分类算法的计算过程：

1）计算待分类点与已知类别的点之间的距离

2）按照距离递增次序排序

3）选取与待分类点距离最小的K个点

4）确定前K个点所在类别的出现次数

5）返回前K个点出现次数最高的类别作为待分类点的预测分类

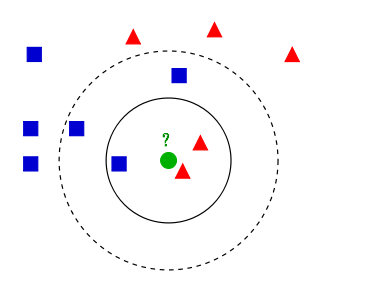
如上图，举个例子：

• 如果K=3，绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
• 如果K=5，绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

二.距离度量选择

1.闵可夫斯基距离

2.欧式距离

3.曼哈顿距离

三.K值的选择

选择较小的K值，容易发生过拟合；选择较大的K值，则容易欠拟合。在应用中，通常采用交叉验证法来选择最优K值。

四.优缺点

优点:

1）算法简单，理论成熟，既可以用来做分类也可以用来做回归。

2）可用于非线性分类。

缺点：

1）需要算每个测试点与训练集的距离，当训练集较大时，计算量相当大，时间复杂度高，特别是特征数量比较大的时候。

2）样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少），对稀有类别的预测准确度低。